MATLAB® Test Report
|
Timestamp: |
31-Oct-2025 13:22:46 |
|
Host: |
runnervmwhb2z |
|
Platform: |
glnxa64 |
|
MATLAB Version: |
24.2.0.2923080 (R2024b) Update 6 |
|
Number of Tests: |
18 |
|
Testing Time: |
28.6552 seconds |
|
Overall Result: |
PASSED |
Overview
/home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/
|
12.2257 seconds |
||
|
|
||
|
16.4294 seconds |
||
|
|
||
Details
/home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/
SmokeTests
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 1.3805 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.1199 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 6.3591 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:20 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_d2a6be97-a4d2-4e45-a4de-d07808b3edf4.png
Event Location: SmokeTests[Project=matlab.project.Project]/SmokeRun(File=IntegratingFactors.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SmokeTests.m (SmokeTests.SmokeRun) at 94 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 1.6266 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:23 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_b1966362-15a4-448b-bc15-018023da5881.png
Event Location: SmokeTests[Project=matlab.project.Project]/SmokeRun(File=SeparationOfVariables.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SmokeTests.m (SmokeTests.SmokeRun) at 94 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 2.6913 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:26 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_3566d373-fdd6-4ac8-b4d4-0acd63a62b20.png
Event Location: SmokeTests[Project=matlab.project.Project]/SmokeRun(File=SystemsOfODEs.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SmokeTests.m (SmokeTests.SmokeRun) at 94 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0483 seconds
(Overview)
SolnSmokeTests
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 0.0685 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.0065 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 0.0055 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 0.0054 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 0.0084 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0055 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 0.0523 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.0742 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 1.3747 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:28 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_3a72e9ba-5f69-4b35-be90-6521985bf1e7.png
Event Location: SolnSmokeTests[Project=matlab.project.Project]/SmokeRun(File=IntegratingFactors.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SolnSmokeTests.m (SolnSmokeTests.SmokeRun) at 110 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 1.3181 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:29 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_f7ac2301-10ef-4856-87e6-1149137cc1c5.png
Event Location: SolnSmokeTests[Project=matlab.project.Project]/SmokeRun(File=SeparationOfVariables.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SolnSmokeTests.m (SolnSmokeTests.SmokeRun) at 110 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 13.4339 seconds
Event:
Diagnostic logged.
|
Timestamp: 31-Oct-2025 13:22:43 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_1ca22349-31c7-4bb2-8820-688569928417.png
Event Location: SolnSmokeTests[Project=matlab.project.Project]/SmokeRun(File=SystemsOfODEs.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SolnSmokeTests.m (SolnSmokeTests.SmokeRun) at 110 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0764 seconds
(Overview)
Command Window Text
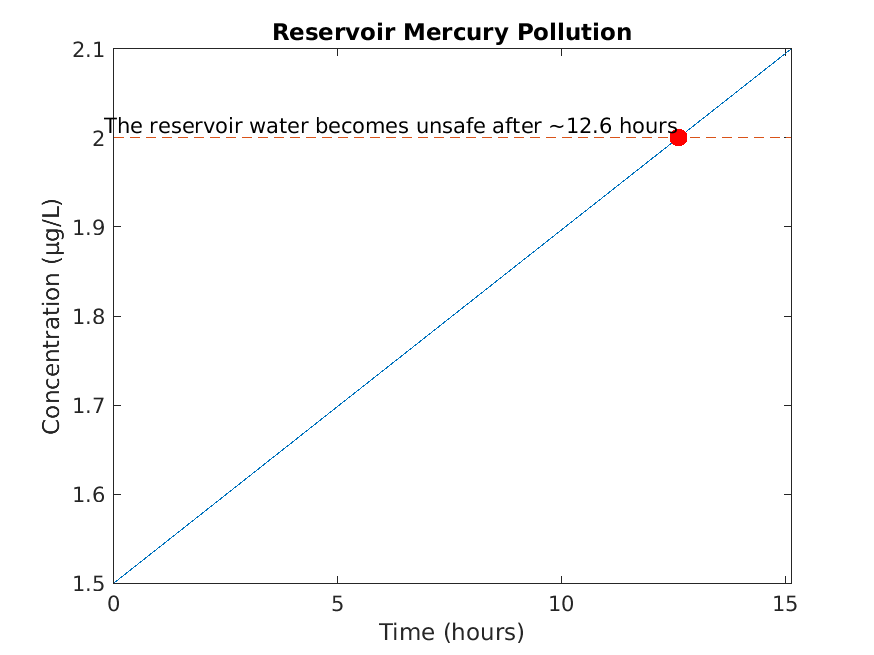
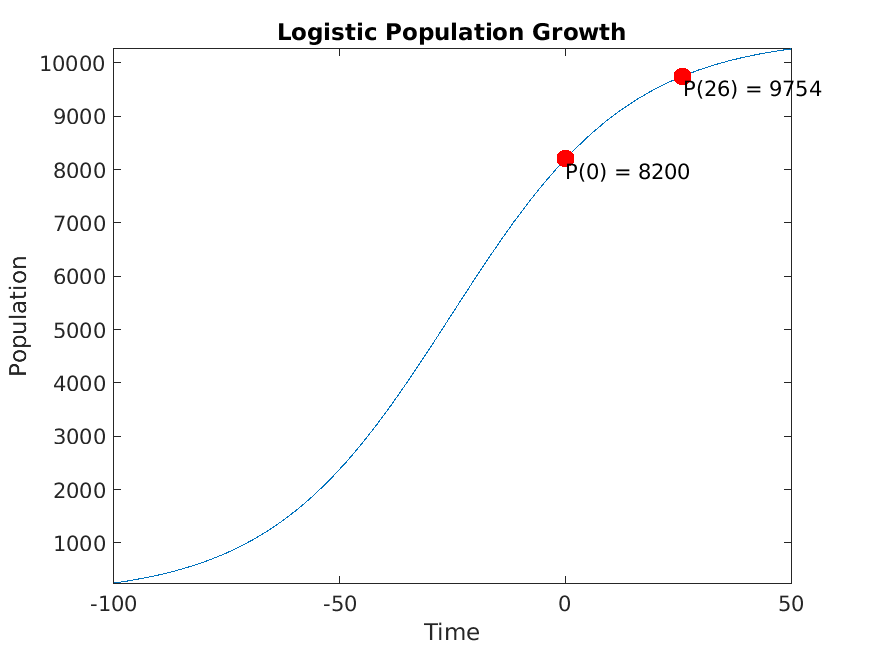
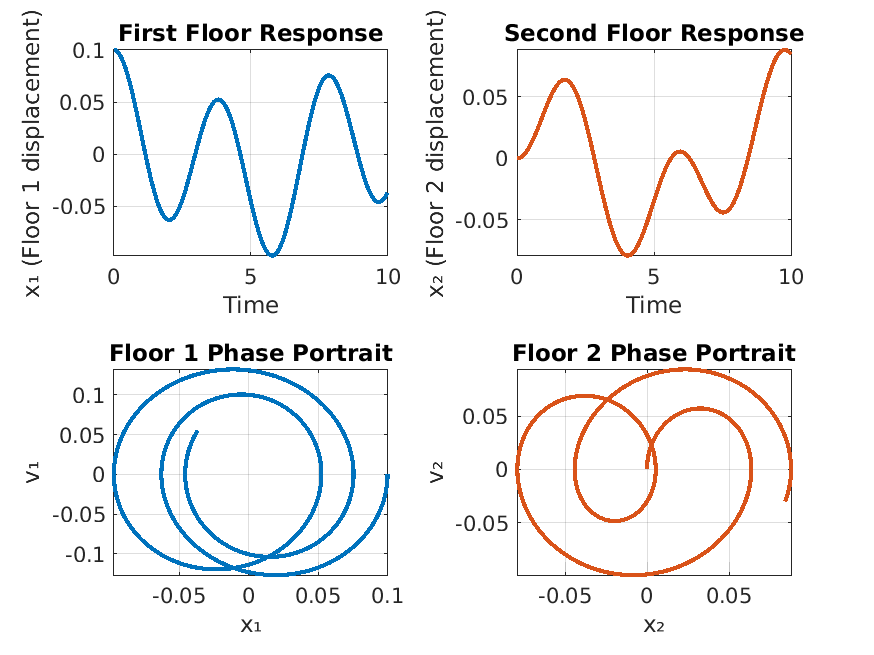
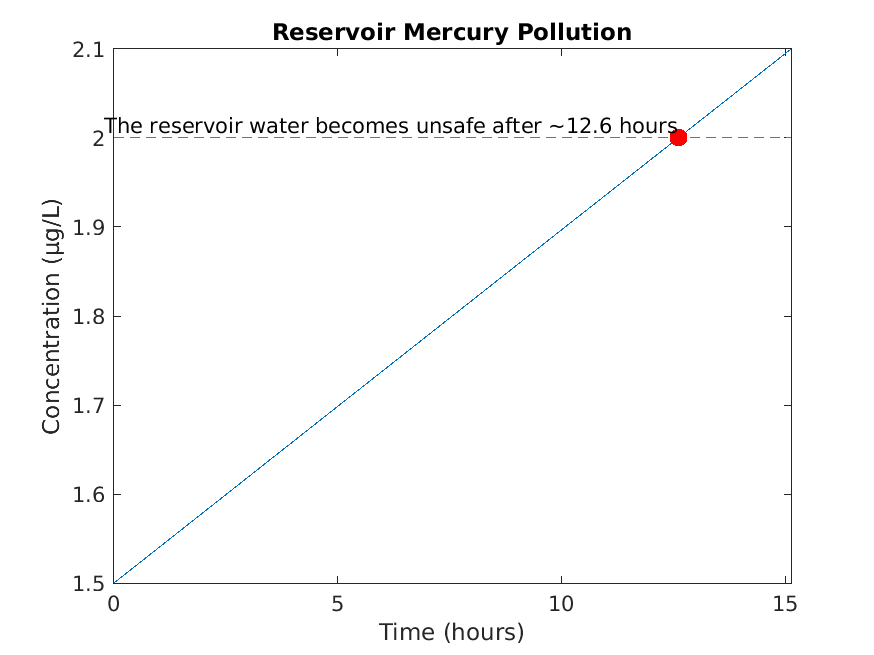
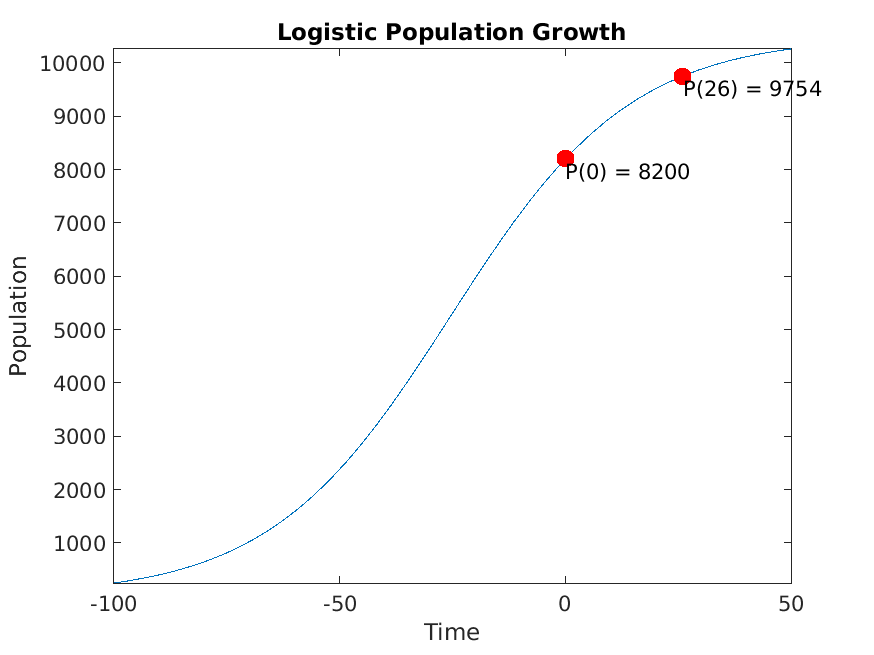
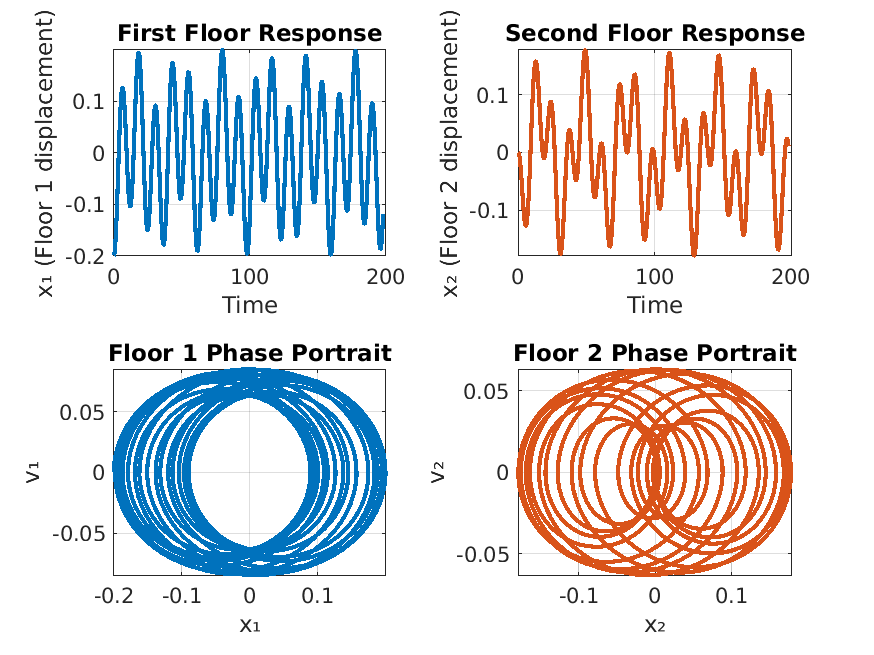
Running SmokeTests >> Running CharacteristicEquations.mlx .>> Running Classification.mlx Please select one or more variables. Please select an answer. Please select one or more variables. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. .>> Running IntegratingFactors.mlx Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a positive integer. We start with our generic formula for chemical concentration: diff(M(t), t) == concentrationIn*rateIn - (rateOut*M(t))/(volInit + t*(rateIn - rateOut)) Plugging in the parameters, we have: diff(M(t), t) == 4 - M(t)/(50*(t/50 + 100)) [Terse] Diagnostic logged (2025-10-31 13:22:20): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_d2a6be97-a4d2-4e45-a4de-d07808b3edf4.png .>> Running SeparationOfVariables.mlx Please select an answer. Please select an answer. Please select an answer. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a positive integer. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. P(t) == (P0*k*exp(r*t))/((k - P0) + P0*exp(r*t)) Plugging in these custom parameters, we get: P(t) == (86100000*exp(t/20))/(8200*exp(t/20) + 2300) Here's a plot of the solution: [Terse] Diagnostic logged (2025-10-31 13:22:23): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_b1966362-15a4-448b-bc15-018023da5881.png .>> Running SystemsOfODEs.mlx Consider the following system of differential equations dx/dt == 3*x + 4*y dy/dt == 4*x + 5*y This is the default. Please enter a non-zero matrix. Please enter the eigenvalues of A. Incorrect. Solve the equation (A - lambda*I)*v == 0 Incorrect. Solve the equation (A - lambda*I)*v == 0 Let beta == 0.6 and gamma == 0.02. Incorrect. In this case, A should be a 2x2 matrix. Please enter the eigenvalues of A. You can be more precise than this. Please select a different answer. Basic reproduction number R₀ = 2 R₀ > 1: Epidemic will occur This is the default. Please enter the correct matrix. This is the default. Please enter the computed eigenvalues. [Terse] Diagnostic logged (2025-10-31 13:22:26): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_3566d373-fdd6-4ac8-b4d4-0acd63a62b20.png .>> Running UndeterminedCoefficients.mlx . Done SmokeTests __________ Running SolnSmokeTests ......>> Running CharacteristicEquationsSoln.mlx .>> Running ClassificationSoln.mlx Correct! b and c are the independent variables in this equation. Correct! This is a partial differential equation, because it has more than one independent variable. Correct! b is the only independent variable in this equation. Correct! This is an ordinary differential equation, because it has one independent variable. Correct! The fourth derivative of y is the highest derivative that appears in the equation, so the order is 4. Correct! All coefficients of y and its derivatatives are constant or functions of t, so the equation is linear. Correct! The trivial solution y=0 is not a solution, so the equation is nonhomogeneous. Correct! The third derivative of y is the highest derivative that appears in the equation, so the order is 3. Correct! The equation has a nonlinear term y' * y, so the equation is nonlinear. Correct! Because the equation is nonlinear, we can't assess its homogeneity. Correct! The second derivative of y is the highest derivative that appears in the equation, so the order is 2. Correct! All coefficients of y and its derivatatives are constant or functions of t, so the equation is linear. Correct! The trivial solution y=0 is a solution, so the equation is homogeneous. .>> Running IntegratingFactorsSoln.mlx Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Starting with the equation from part (c): M == (20000*t + 2*t^2 + C)/(5000 + t) Remember that M represents the *quantity* of mercury in the water, so we have M(0) = 1.5 * 100 = 150. Solve for C, plugging in M = 150 and t = 0: 150 == (0 + 0 + C)/(5000 + 0) 150 == C/5000 C == 750000 Finally, plugging this value for C back into the equation from part (c), we get: M == (20000*t + 2*t^2 + 750000)/(5000 + t) Correct! See below for a detailed explanation. We start with our generic formula for chemical concentration: diff(M(t), t) == concentrationIn*rateIn - (rateOut*M(t))/(volInit + t*(rateIn - rateOut)) Plugging in the parameters, we have: diff(M(t), t) == 4 - M(t)/(50*(t/50 + 100)) [Terse] Diagnostic logged (2025-10-31 13:22:28): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_3a72e9ba-5f69-4b35-be90-6521985bf1e7.png .>> Running SeparationOfVariablesSoln.mlx Correct! This can be rewritten as: (1/y)*dy == 3*x^2*dx Correct! Using y' = dy/dx, this can be rewritten as: (1/y^2)*dy == (e^x/x)*dx Correct! There is no way to separate the x and y terms in this equation, so it is not separable. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. P(t) == (P0*k*exp(r*t))/((k - P0) + P0*exp(r*t)) Plugging in these custom parameters, we get: P(t) == (86100000*exp(t/20))/(8200*exp(t/20) + 2300) Here's a plot of the solution: [Terse] Diagnostic logged (2025-10-31 13:22:29): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_f7ac2301-10ef-4856-87e6-1149137cc1c5.png . >> Running SystemsOfODEsSoln.mlx Consider the following system of differential equations dx/dt == - 2*x + 5*y dy/dt == x + 5*y Correct! The system dx/dt == - 2*x + 5*y dy/dt == x + 5*y can be written as: matrix([[dx/dt], [dy/dt]]) == matrix([[-2, 5], [1, 5]])*matrix([[x], [y]]) So A == matrix([[-2, 5], [1, 5]]) Correct! To find eigenvalues, solve det(A - lambda*I) == 0: det(matrix([[- lambda - 2, 5], [1, - lambda + 5]])) == 0 - 3*lambda + lambda^2 - 15 == 0 lambda_1 == (3 + sqrt((-3)^2 - (-60)))/2, lambda_1 == 69^(1/2)/2 + 3/2 lambda_2 == (3 - sqrt((-3)^2 - (-60)))/2, lambda_2 == - 69^(1/2)/2 + 3/2 For lambda == 69^(1/2)/2 + 3/2, solve (A - lambda*I)*v == 0 matrix([[- 69^(1/2)/2 - 7/2, 5], [1, - 69^(1/2)/2 + 7/2]])*matrix([[v_1], [v_2]]) == matrix([[0], [0]]) matrix([[v_1], [v_2]]) == matrix([[69^(1/2)/2 - 7/2], [1]]) For lambda == - 69^(1/2)/2 + 3/2, solve (A - lambda*I)*v == 0 matrix([[69^(1/2)/2 - 7/2, 5], [1, 69^(1/2)/2 + 7/2]])*matrix([[v_1], [v_2]]) == matrix([[0], [0]]) matrix([[v_1], [v_2]]) == matrix([[- 69^(1/2)/2 - 7/2], [1]]) x(t) == - c_1*exp(-t*(69^(1/2)/2 - 3/2))*(69^(1/2)/2 + 7/2) + c_2*exp(t*(69^(1/2)/2 + 3/2))*(69^(1/2)/2 - 7/2) y(t) == c_1*exp(-t*(69^(1/2)/2 - 3/2)) + c_2*exp(t*(69^(1/2)/2 + 3/2)) Checking... matrix([[c_1*exp(-t*(69^(1/2)/2 - 3/2))*(69^(1/2)/2 - 3/2)*(69^(1/2)/2 + 7/2) + c_2*exp(t*(69^(1/2)/2 + 3/2))*(69^(1/2)/2 + 3/2)*(69^(1/2)/2 - 7/2)], [c_2*exp(t*(69^(1/2)/2 + 3/2))*(69^(1/2)/2 + 3/2) - c_1*exp(-(t*(69^(1/2) - 3))/2)*(69^(1/2)/2 - 3/2)]]) - matrix([[-2, 5], [1, 5]])*matrix([[- c_1*exp(-t*(69^(1/2)/2 - 3/2))*(69^(1/2)/2 + 7/2) + c_2*exp(t*(69^(1/2)/2 + 3/2))*(69^(1/2)/2 - 7/2)], [c_1*exp(-t*(69^(1/2)/2 - 3/2)) + c_2*exp(t*(69^(1/2)/2 + 3/2))]]) == matrix([[0], [0]]) Let beta == 0.2 and gamma == 0.2. Plugging in the values for beta == 0.2 and gamma == 0.2 we see that we get: Correct! The system dS/dt == -0.2*I dI/dt == 0 which can be written as matrix([[dS/dt], [dI/dt]]) == matrix([[0, -0.2], [0, 0]])*matrix([[S], [I]]) So A == matrix([[0, -0.2], [0, 0]]) Correct! To find eigenvalues, solve det(A - lambda*I) == 0: det(matrix([[-1.0*lambda, -0.2], [0, -1.0*lambda]])) == 0 lambda^2 == 0 lambda_1 == (0.0 + sqrt(0.0^2 - 0.0))/2.0, lambda_1 == 0.0 lambda_2 == (0.0 - sqrt(0.0^2 - 0.0))/2.0, lambda_2 == 0.0 Correct! Zero eigenvalues indicate marginal stability - small perturbations neither grow nor decay exponentially. Basic reproduction number R₀ = 1 The disease is endemic in the population. Correct! The coefficient matrix represents the building dynamics. A == matrix([[0, 1, 0, 0], [-2*omega^2, 0, omega^2, 0], [0, 0, 0, 1], [omega^2, 0, -omega^2, 0]]) dx_1/dt == v_1 dv_1/dt == - 2*omega^2*x_1 + omega^2*x_2 dx_2/dt == v_2 dv_2/dt == omega^2*x_1 - omega^2*x_2 Correct! The eigenvalues are ±(- 5^(1/2)/2 - 3/2)^(1/2) and ±(5^(1/2)/2 - 3/2)^(1/2), or approximately ±1.618i and ±0.618i, representing the natural frequencies of the building modes. The characteristic equation is: lambda^4 + 3*lambda^2 + 1 == 0 [Terse] Diagnostic logged (2025-10-31 13:22:43): Figure saved to: --> /tmp/7479888e-d426-4978-a427-3016021368c0/Figure_1ca22349-31c7-4bb2-8820-688569928417.png .>> Running UndeterminedCoefficientsSoln.mlx . Done SolnSmokeTests __________