MATLAB® Test Report
|
Timestamp: |
05-Mar-2025 18:22:28 |
|
Host: |
fv-az1436-346 |
|
Platform: |
glnxa64 |
|
MATLAB Version: |
24.1.0.2837808 (R2024a) Update 7 |
|
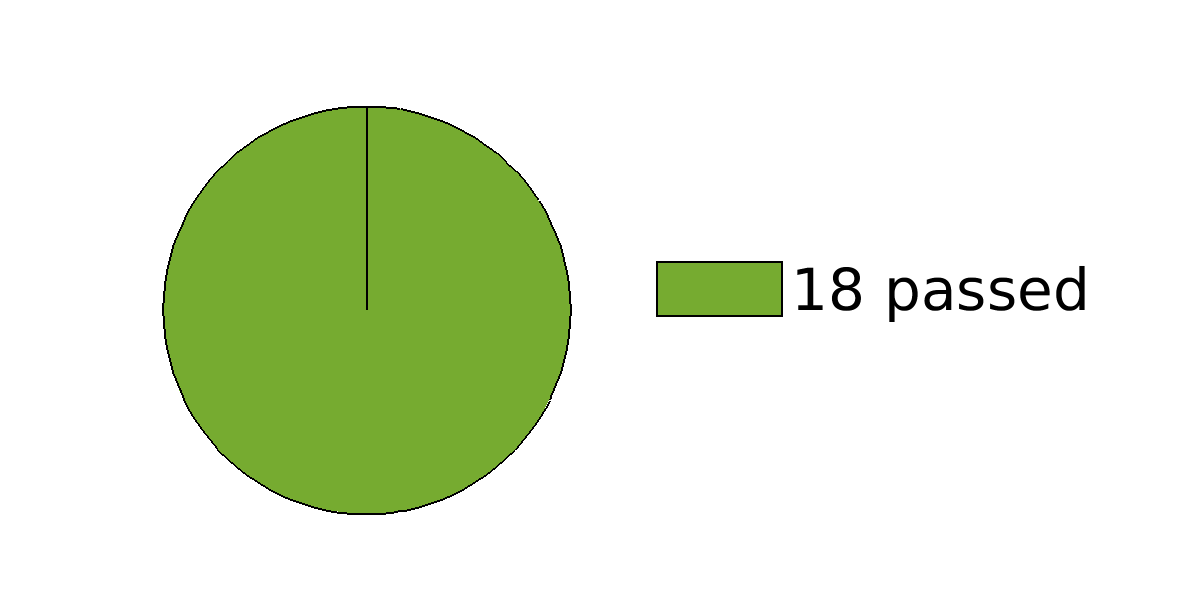
Number of Tests: |
18 |
|
Testing Time: |
12.7159 seconds |
|
Overall Result: |
PASSED |
Overview
/home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/
|
10.1206 seconds |
||
|
|
||
|
2.5953 seconds |
||
|
|
||
Details
/home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/
SmokeTests
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 1.2085 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.1776 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 7.0508 seconds
Event:
Diagnostic logged.
|
Timestamp: 05-Mar-2025 18:22:19 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_ca98877c-302c-4a49-bc26-e9217d36deab.png
Event Location: SmokeTests[Project=matlab.project.Project]/SmokeRun(File=IntegratingFactors.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SmokeTests.m (SmokeTests.SmokeRun) at 94 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 1.5837 seconds
Event:
Diagnostic logged.
|
Timestamp: 05-Mar-2025 18:22:22 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_98534b31-7a23-4d83-ab77-5e741da78ebd.png
Event Location: SmokeTests[Project=matlab.project.Project]/SmokeRun(File=SeparationOfVariables.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SmokeTests.m (SmokeTests.SmokeRun) at 94 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 0.0674 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0326 seconds
(Overview)
SolnSmokeTests
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 0.0431 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.0057 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 0.0050 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 0.0050 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 0.0070 seconds
(Overview)
ExistSolns
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0051 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=CharacteristicEquations.mlx
The test passed. Duration: 0.0428 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=Classification.mlx
The test passed. Duration: 0.0491 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=IntegratingFactors.mlx
The test passed. Duration: 1.3966 seconds
Event:
Diagnostic logged.
|
Timestamp: 05-Mar-2025 18:22:24 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_077cc758-b7d7-4557-95e3-6c4f89c9ded4.png
Event Location: SolnSmokeTests[Project=matlab.project.Project]/SmokeRun(File=IntegratingFactors.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SolnSmokeTests.m (SolnSmokeTests.SmokeRun) at 110 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SeparationOfVariables.mlx
The test passed. Duration: 0.9644 seconds
Event:
Diagnostic logged.
|
Timestamp: 05-Mar-2025 18:22:25 Verbosity: Terse Logged Diagnostic: Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_c0661fc6-feca-4771-a219-34b64dee2498.png
Event Location: SolnSmokeTests[Project=matlab.project.Project]/SmokeRun(File=SeparationOfVariables.mlx) Stack: In /home/runner/work/Applied-ODEs/Applied-ODEs/SoftwareTests/SolnSmokeTests.m (SolnSmokeTests.SmokeRun) at 110 |
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=SystemsOfODEs.mlx
The test passed. Duration: 0.0396 seconds
(Overview)
SmokeRun
Class Setup Parameters: Project=matlab.project.Project
Test Parameters: File=UndeterminedCoefficients.mlx
The test passed. Duration: 0.0319 seconds
(Overview)
Command Window Text
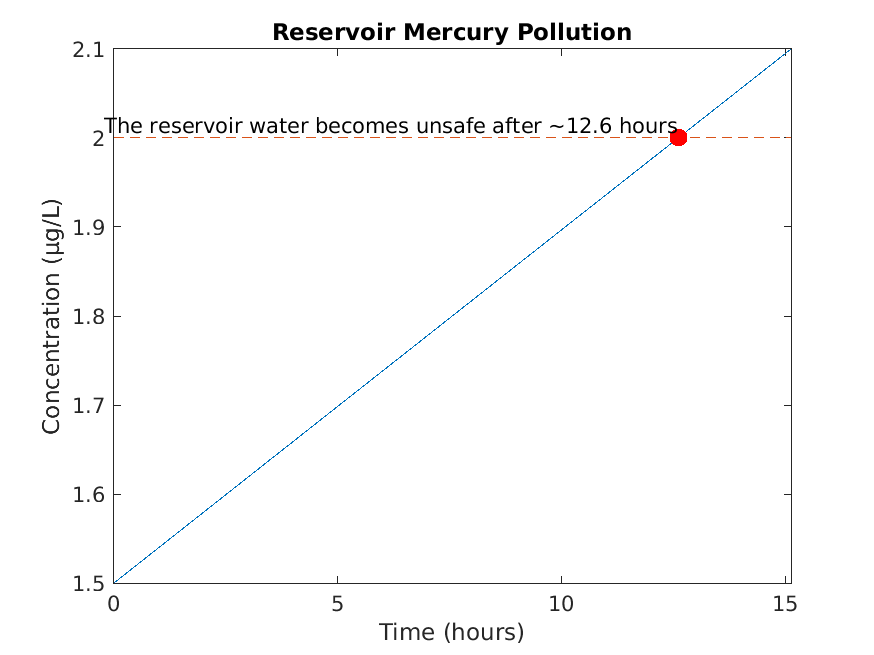
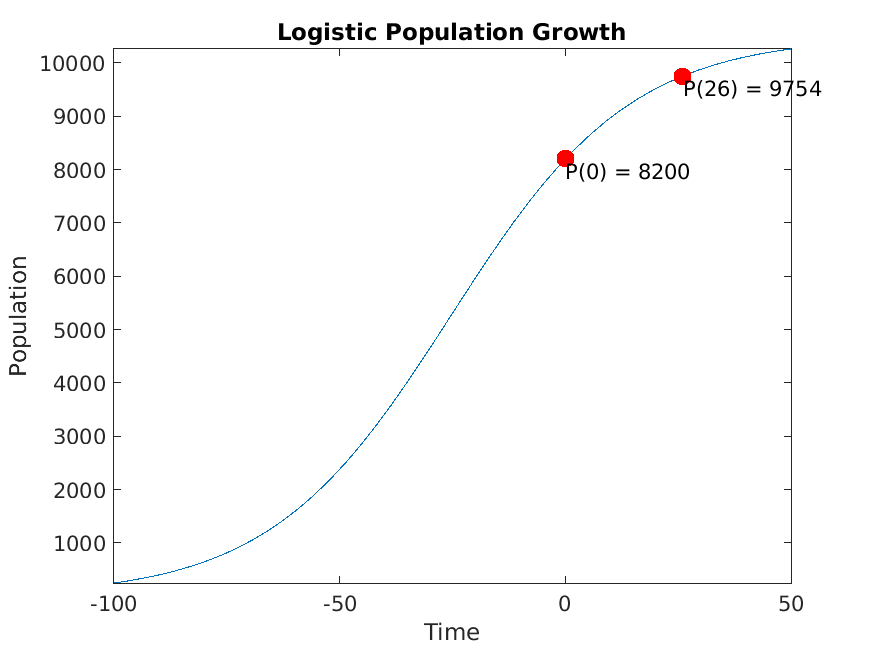
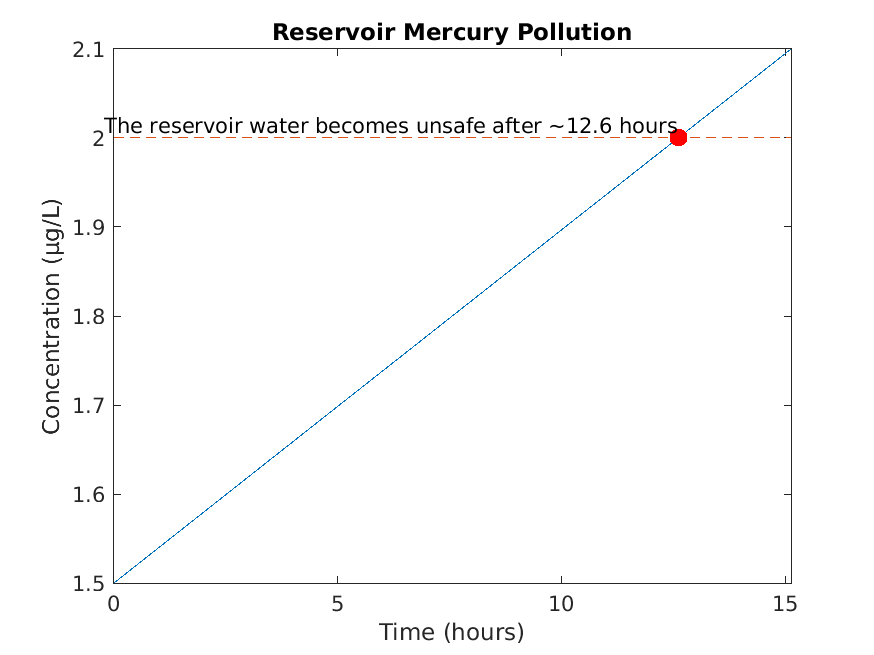
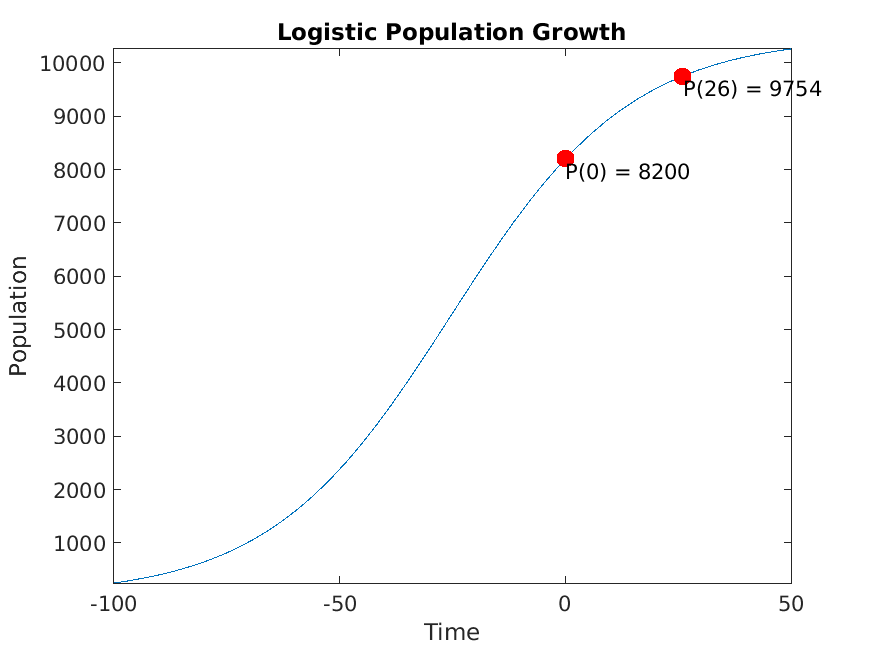
Running SmokeTests >> Running CharacteristicEquations.mlx .>> Running Classification.mlx Please select one or more variables. Please select an answer. Please select one or more variables. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. Please enter a nonzero order. Please select an answer. Please select an answer. .>> Running IntegratingFactors.mlx Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a positive integer. We start with our generic formula for chemical concentration: diff(M(t), t) == concentrationIn*rateIn - (rateOut*M(t))/(volInit + t*(rateIn - rateOut)) Plugging in the parameters, we have: diff(M(t), t) == 4 - M(t)/(50*(t/50 + 100)) [Terse] Diagnostic logged (2025-03-05 18:22:19): Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_ca98877c-302c-4a49-bc26-e9217d36deab.png .>> Running SeparationOfVariables.mlx Please select an answer. Please select an answer. Please select an answer. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a positive integer. Please enter a nonzero expression. Please enter a nonzero expression. Please enter a nonzero expression. P(t) == (P0*k*exp(r*t))/((k - P0) + P0*exp(r*t)) Plugging in these custom parameters, we get: P(t) == (86100000*exp(t/20))/(8200*exp(t/20) + 2300) Here's a plot of the solution: [Terse] Diagnostic logged (2025-03-05 18:22:22): Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_98534b31-7a23-4d83-ab77-5e741da78ebd.png .>> Running SystemsOfODEs.mlx .>> Running UndeterminedCoefficients.mlx . Done SmokeTests __________ Running SolnSmokeTests ......>> Running CharacteristicEquationsSoln.mlx .>> Running ClassificationSoln.mlx Correct! b and c are the independent variables in this equation. Correct! This is a partial differential equation, because it has more than one independent variable. Correct! b is the only independent variable in this equation. Correct! This is an ordinary differential equation, because it has one independent variable. Correct! The fourth derivative of y is the highest derivative that appears in the equation, so the order is 4. Correct! All coefficients of y and its derivatatives are constant or functions of t, so the equation is linear. Correct! The trivial solution y=0 is not a solution, so the equation is nonhomogeneous. Correct! The third derivative of y is the highest derivative that appears in the equation, so the order is 3. Correct! The equation has a nonlinear term y' * y, so the equation is nonlinear. Correct! Because the equation is nonlinear, we can't assess its homogeneity. Correct! The second derivative of y is the highest derivative that appears in the equation, so the order is 2. Correct! All coefficients of y and its derivatatives are constant or functions of t, so the equation is linear. Correct! The trivial solution y=0 is a solution, so the equation is homogeneous. .>> Running IntegratingFactorsSoln.mlx Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Starting with the equation from part (c): M == (20000*t + 2*t^2 + C)/(5000 + t) Remember that M represents the *quantity* of mercury in the water, so we have M(0) = 1.5 * 100 = 150. Solve for C, plugging in M = 150 and t = 0: 150 == (0 + 0 + C)/(5000 + 0) 150 == C/5000 C == 750000 Finally, plugging this value for C back into the equation from part (c), we get: M == (20000*t + 2*t^2 + 750000)/(5000 + t) Correct! See below for a detailed explanation. We start with our generic formula for chemical concentration: diff(M(t), t) == concentrationIn*rateIn - (rateOut*M(t))/(volInit + t*(rateIn - rateOut)) Plugging in the parameters, we have: diff(M(t), t) == 4 - M(t)/(50*(t/50 + 100)) [Terse] Diagnostic logged (2025-03-05 18:22:24): Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_077cc758-b7d7-4557-95e3-6c4f89c9ded4.png .>> Running SeparationOfVariablesSoln.mlx Correct! This can be rewritten as: (1/y)*dy == 3*x^2*dx Correct! Using y' = dy/dx, this can be rewritten as: (1/y^2)*dy == (e^x/x)*dx Correct! There is no way to separate the x and y terms in this equation, so it is not separable. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. Correct! See below for a detailed explanation. P(t) == (P0*k*exp(r*t))/((k - P0) + P0*exp(r*t)) Plugging in these custom parameters, we get: P(t) == (86100000*exp(t/20))/(8200*exp(t/20) + 2300) Here's a plot of the solution: [Terse] Diagnostic logged (2025-03-05 18:22:25): Figure saved to: --> /tmp/f6e5325b-183e-4c9d-880e-068a46f15687/Figure_c0661fc6-feca-4771-a219-34b64dee2498.png . >> Running SystemsOfODEsSoln.mlx .>> Running UndeterminedCoefficientsSoln.mlx . Done SolnSmokeTests __________